Evolving
Life moves in spirals.
New growth. Experiences.
Cowlicks. Galaxies.
The Fibonacci Sequence is a basic building block in nature. It forms a geometry such as that of a nautilus shell and results in the Fibonacci Spiral. The sequence is 1, 1, 2, 3, 5, 8, 13, 21, 34, 55….. Each number is added to the preceding number to get the next number in the sequence.
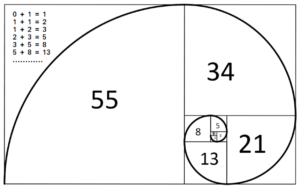 The Fibonacci Spiral is related to the Golden Ratio of sacred geometry (Phi = 1.618…). However, there is a significant difference that alters everything: The Golden Ratio is infinite. In other words, it has no beginning and no end. It is perfection, The Source, God.
The Fibonacci Spiral is related to the Golden Ratio of sacred geometry (Phi = 1.618…). However, there is a significant difference that alters everything: The Golden Ratio is infinite. In other words, it has no beginning and no end. It is perfection, The Source, God.
The Fibonacci Spiral, on the other hand, is Nature’s way of replicating the infinite Golden Ratio in our finite world (the Cosmos) where everything – everything – has a beginning and an end. In this case, the beginning is 1, 1. One egg and one sperm, for example.
We see this repeating pattern again and again in the natural world. Just a few examples are the pine cone, a hurricane, a sunflower, the reproduction of rabbits, spiral galaxies, the proportions of the human body, music….
Speaking of music, one immediate way we see the ratio on the piano is that an octave has 5 black keys and 8 white keys and together they equal 13. We see the number 5 represented in the famous da Vinci drawing, Vitruvian Man, showing the proportions of the finite human body. And, when turned sideways, 8 represents infinity.
On a different note, I recently heard a piano piece where the musician has composed a song using the numbers of the Fibonacci Sequence. It’s Beautiful. Enjoy!
These two similar geometries that have only one significant difference, a difference that changes everything, are a reminder of the connection between infinite and finite in our lives. The Fibonacci Sequence allows us to physically see and experience a pattern of perfection that is beyond the physical world (the Cosmos). What a Grand Design!
 Also, I designed this set of prayer beads using the Fibonacci Sequence as my guide. You can read about them here.
Also, I designed this set of prayer beads using the Fibonacci Sequence as my guide. You can read about them here.

